1002번: 터렛
각 테스트 케이스마다 류재명이 있을 수 있는 위치의 수를 출력한다. 만약 류재명이 있을 수 있는 위치의 개수가 무한대일 경우에는 -1을 출력한다.
www.acmicpc.net
두 원의 중심과 두 원의 교차점과 한 원의 중심점 사이의 거리가 두 개 주어졌을 때 만들 수 있는 원을 생각하고 이렇게 생긴 두 개의 원이 겹침으로써 만들어지는 교차점의 개수를 구하는 문제였습니다.
풀이방법
1. 값 구하기 : 주어진 두 원의 중심의 점으로 거리를 구할 수 있습니다. 이를 변수 a로 정의합니다. 다음은 (x1,y1) , (x2,y2) 사이의 거리를 구하는 공식입니다.
$$a = \sqrt{(x1-x2)^2 + (y1-y2)^2} $$
이후 각 반지름 r1과 r2의 값을 각각 b, c변수에 저장합니다.
2. 경우에 따라 값을 출력합니다.
2-1. a가 0일 때 : 이 경우는 두 원의 중심이 같을 경우입니다.
이 때 만약 b == c 라면 이 때는 완전히 같은 원이 되므로 류재명이 있을 수 있는 좌표는 무한대입니다. 따라서 -1을 출력합니다.
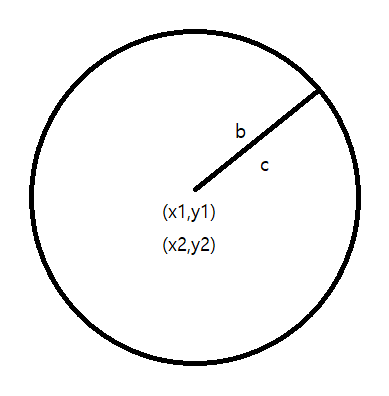
b != c라면 동심원 즉 원의 중심은 같지만 반지름만 다른 원이 되므로 이 때는 교차점이 0개이므로 0을 출력합니다.
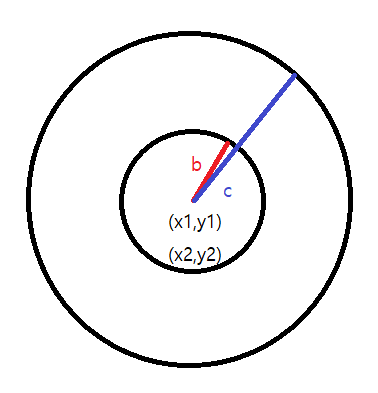
선이 겹치면 잘 보이지 않아 부득이 하게 약간 비뚫게 그렸지만 원래는 같은 대상에 대한 거리를 다른 사람이 계산 한 값이기 때문에 파란선과 빨간선이 일직선상에 놓여있다고 생각하시면 됩니다.
2-2. a가 0이 아닐 때 : 이 경우는 두 원의 중심이 다를 경우입니다.
이 경우엔 크게 3가지의 경우로 나뉩니다.
두 원의 중심이 다르고 두 원 중심사이의 거리가 각 원의 중심으로부터 류재명까지의 거리의 합보다 작다면 원이 겹쳐있다고 생각할 수 있습니다. 하지만 이는 원의 반지름에 따라 결과값은 달라질 수 있습니다. 따라서 만들 수 있는 원들을 여러가지로 생각해 보아야 합니다.

이 경우를 살펴보면 아무리 조정을 해도 c > a + b일 수가 없다는 것을 알 수 있습니다. 이는 a,b,c를 각각 한 변으로 생각했을 때 삼각형을 이루므로 삼각형을 이룰 수 있는 조건을 생각한다면 도출할 수 있는 결론입니다. 따라서 다음과 같은 식을 세워볼 수 있습니다. a + min(b,c) < max(b,c)일 때는 교차점이 0
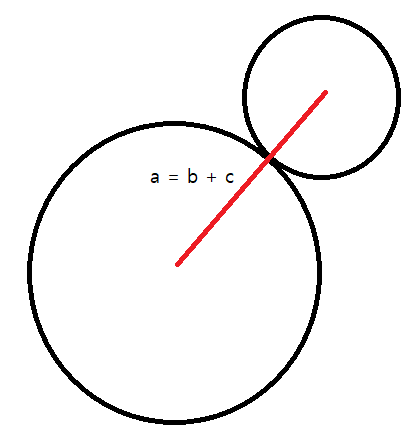
이 경우에는 교차점이 1개입니다. 따라서 식을 세워보면 a + min(b,c) == max(b,c) 일 때 교차점은 1
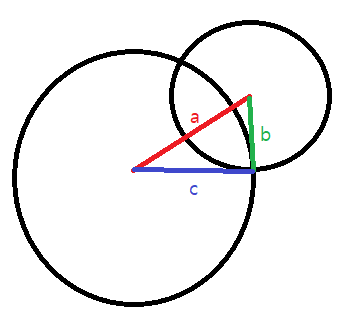
이 경우에는 교차점이 2개입니다.
이렇게 a가 가장 큰 변으로 나타냈으나 a가 제일 작은 변이 되거나 중간 크기의 변일 수도 있습니다. 이런 경우를 모두 고려하여 작성해야합니다.
Code
#include <iostream>
#include <cmath>
using namespace std;
int main(){
int t;
cin >> t;
while(t--){
int x1,y1,r1,x2,y2,r2;
cin >> x1 >> y1 >> r1 >> x2 >> y2 >> r2;
double a = sqrt((abs(x1-x2)) * (abs(x1-x2)) + (abs(y1-y2)) * (abs(y1-y2)));
double b = r1;
double c = r2;
//cout << "a, b, c : " << a << ' ' << b << ' ' << c << '\n';
if(!a){
if(b == c) cout << -1 << '\n';
else cout << 0 <<'\n';
}
else{
if(a < b + c){
if(a + min(b,c) == max(b,c)) cout << 1 <<'\n';
else if(a + min(b,c) < max(b,c)) cout << 0 << '\n';
else cout << 2 <<'\n';
}
else if(a == b + c) cout << 1 << '\n';
else cout << 0 << '\n';
}
}
}
'Algorithm > Math' 카테고리의 다른 글
| (C++) - 프로그래머스(연습문제) : 최솟값 만들기 (0) | 2021.04.04 |
|---|---|
| (C++) - 백준(BOJ) 1673번 : 치킨쿠폰 (0) | 2021.03.18 |
| (C++) - 프로그래머스(연습문제) : 행렬의 곱셈 (0) | 2021.03.06 |
| (C++) - 프로그래머스(연습문제) : 최대공약수와 최소공배수 (0) | 2021.03.05 |
| (C++) - 프로그래머스(연습문제) : 소수찾기 (0) | 2021.03.01 |