https://www.acmicpc.net/problem/2021
2021번: 최소 환승 경로
첫째 줄에 역의 개수 N(1≤N≤100,000), 노선의 개수 L(1≤L≤100,000)이 주어진다. 다음 L개의 줄에는 각 노선이 지나는 역이 순서대로 주어지며 각 줄의 마지막에는 -1이 주어진다. 마지막 줄에는 출발
www.acmicpc.net
5214번과 같은 bfs 문제였습니다.
📕 풀이방법
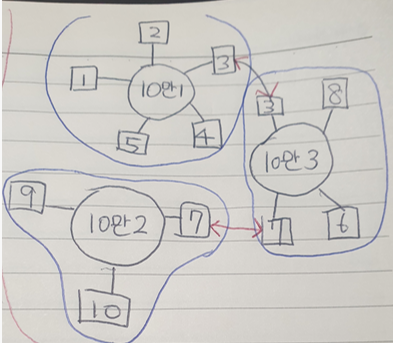
같은 호선에 속해있는 역끼리는 간선으로 연결할 필요가 없습니다. 유의미한 간선은 역 <-> 호선 또는 호선 <-> 역 뿐입니다. 인접그래프를 형성할 때 정점을 역, 호선으로 생각하며 역과 호선 사이를 간선으로 해 형성해줍니다. 호선은 동그라미, 역은 네모로 그림을 그렸습니다. 이렇게 간선의 개수를 줄일 수 있습니다.
이제 탐색할 때를 생각해봅니다. 파란색선 안쪽 영역은 어떻게 이동해도 비용이 0이고 다른 호선으로 환승할 때만 비용이 1이 든다고 볼 수 있습니다.
📔 입력 및 초기화
m개의 호선에 대해 각 호선에 속한 정점들을 k개씩 입력하고 무방향 인접리스트를 형성해줍니다. 호선 i번 호선 입력시 i에 10만을 더해 다른 정점 혹은 호선과 겹치는 수가 발생하지 않도록 주의합니다.
📔 풀이과정
1번 정점을 시작점으로 하는 bfs를 수행합니다.
1. 1번 정점을 방문했으므로 dist[1] = 1입니다. 그 후 시작점 1을 queue에 push해줍니다.
2. x정점이 n이라면 도착했으므로 dist[x]를 반환해줍니다.
3. x정점에서 인접 정점(next)들 중 처음 방문했을 때 환승역라면 dist[next] = dist[x] + 1입니다.
다음 정점이 일반 정점이라면 최소거리가 아니기 때문에 dist[next] = dist[x]입니다. 같은 호선에 속한 역끼리는 이동하면 손해이기 때문에 가중치가 없다고 생각해야 합니다.
4. 모든 정점을 확인했음에도 도착하지 못했다면 -1을 반환합니다.
📔 정답출력
bfs함수의 반환값을 출력합니다.
📕 Code
#include <bits/stdc++.h>
using namespace std;
int n, m, s, e;
vector<int> route[200001];
int dist[200001];
int bfs(){
queue <int> q;
dist[s] = 0;
q.push(s);
while(!q.empty()){
int x = q.front();
q.pop();
if(x == e) return dist[x] - 1 > 0 ? dist[x] - 1 : 0;
for(auto next : route[x]) {
if(dist[next] > -1) continue;
if(next > 100000) dist[next] = dist[x] + 1;
else dist[next] = dist[x];
q.push(next);
}
}
return -1;
}
int main(){
memset(dist,-1,sizeof(dist));
cin >> n >> m;
for(int i = 1; i <= m; i++){
while(1){
int v;
cin >> v;
if(v == -1) break;
route[v].push_back(i+100000);
route[i+100000].push_back(v);
}
}
cin >> s >> e;
cout << bfs();
}
'Algorithm > BFS' 카테고리의 다른 글
| (C++) - 백준(BOJ) 3197번 : 백조의 호수 (0) | 2021.08.27 |
|---|---|
| (C++) - 백준(BOJ) 16954번 : 움직이는 미로 탈출 (0) | 2021.08.23 |
| (C++) - 백준(BOJ) 5214번 : 환승 (0) | 2021.08.17 |
| (C++) - 백준(BOJ) 15723번 : n단 논법 (0) | 2021.08.12 |
| (C++) - 백준(BOJ) 1240번 : 노드사이의 거리 (0) | 2021.08.09 |